Declarative programming is the use of unsequenced statements that are performed in response to external stimuli. In circuit design, this style of programming usually appears as constraints that are attached to a design. There is no linear flow of control because the sequencing of these constraints is dependent on the structure of the circuit. Nevertheless, such code is powerful enough to perform any function. Many declarative languages are textual [Kingsley; Johnson; Lipton et al.; Davis and Clark], but these languages place their constraints on spatially located objects, thus functioning in a similar way to graphical languages.
Constraints can be used for a number of purposes. In layout systems, they commonly hold together pieces of the circuit so that the geometry will be correct. Textual constraint languages, which typically are evaluated in a batch mode, consider all constraints at once and produce a completed physical layout. Graphical constraint languages are more interactive, allowing continuous changes to the constraints and the geometry. Such systems demand incremental evaluation of declarative code so that, as changes are made, the constraints adjust appropriate components and wires. This is the situation in the Electric design system which has constraining wires that keep all components connected (see Chapter 11).
Although constraints are typically applied to geometry, they can also be used for other purposes. In VLSI design, many relevant pieces of circuit information can be coded as constraints. The Palladio system [Brown, Tong, and Foyster] has constraints for restricted interconnect so that components will be properly placed with respect to power, ground, input, output, clocks, restored signals, and so on. Other systems make use of timing constraints [Arnold; Borriello] or arbitrary code constraints that can respond to any need [Zippel].
In totally unrestricted constraint systems, users can write their own code to manipulate the circuit. These systems allow constraints on any value in the database so that code can be executed whenever necessary. This is implemented by having each attribute contain an optional code slot that executes when the attribute changes. Such systems can do arbitrary functions, such as hierarchical simulation [Saito, Uehara, and Kawato].
| One difference between declarative and imperative programs is that there is no clear sequence of execution in a declarative constraint system. This means that the constraint-solving method is crucial to proper execution, and different solution methods will produce different results. Consider the four constraints in Fig. 8.6. If the constraint solver begins with object A, it has a choice of satisfying two constraints. Choosing the above constraint will place object B below object A. Now there is a choice between finishing the other constraint on A and proceeding with the constraint on B. If the solver chooses to go on to B, it will place object C to the right of B by three units. However, if it continues in this order, and places object D according to the constraint on C, it will be unable to satisfy the second constraint on object A because D will be too close. |
|
This example illustrates many issues in constraint satisfaction. The basic problem in the example is that there is a constraint loop. Although this particular loop is easily solved in a number of ways, not all loops can be solved. In fact, overconstrained situations occur in which loops cannot be resolved because the constraints contradict each other. Detection of these loops requires some form of constraint marking to prevent infinite reevaluation. Once it detects these loops, the system must be prepared to deal with them in an appropriate manner. For VLSI design, in which each connection is a signal path, it is better to change the constraints than to change the topology.
| The basic method of solving constraint loops, called backtracking, requires reversal of constraint execution until a point is reached at which an alternative choice will work. A stack must be kept with all the premises for each constraint decision so that it is possible to know how far to back up [Steele; Stallman and Sussman]. It may take many steps of backtracking to find the correct solution, and even simple backtracking may not be possible if unforeseen constraints continue to affect the search (see Fig. 8.7). Also, backtracking is time consuming. |
|
In some situations it is possible to remove loops by precomputing their characteristics and reducing them to simpler constraints [Gosling]. Such loop transformation involves the creation of a new constraint that acts like the old one but has the loop conflict resolved. This is done by algebraically manipulating the expressions that compose the original constraints to eliminate references to internal loop state and produce a set of equations that fully describe their characteristics.
As an alternative to computationally expensive solution methods, there are some simple techniques that can make constraints easier to solve. For example, it may be possible to prioritize the constraints according to their effects on other constraints, and to use this to obtain improved sequencing. In the example of Fig. 8.6, the constraint left by 5 is more restrictive than is below and should be solved first to ensure consistency. Another feature that may help solve constraints is the ability to work them from any known point to the other, unknown points. This allows the solver to execute all constraints at any point, without having to work around a loop. In constraints that involve more than two objects, it should be possible to derive any value, given the others. If this is not possible, the user should be encouraged to add new constraints that are equivalent to the existing set but provide new opportunities for solution [Borning; Steele]. An alternative to adding new constraints is to have multiple views of a circuit with totally different ways of evaluating constraint systems [Sussman].
Another issue in sequencing constraints is the distinction between breadth-first and depth-first search. The example of Fig. 8.6 chose depth-first sequencing when it evaluated the constraint on object B before finishing the constraints on object A. Thus it went deeper into the constraint tree before finishing the constraints at the current level. Depth-first sequencing is used when the consequences of any one constraint must be fully known before other constraints can be evaluated. Breadth-first is used when the environment of a particular object is more important than that of others, and all constraints on that object must be evaluated first. It is not unreasonable to switch between the two types of search depending on the nature of the constraints found, using depth for important constraints and then finishing the less important ones by breadth. Care must be taken to ensure that all constraints get their turn.
As an example of implementing a constraint system, a simple geometric-constraint solver will be described. This particular technique, based on linear inequalities, is very popular and can be found in the textual design languages Plates [Sastry and Klein], EARL [Kingsley], ALI [Lipton et al.], LAVA [Mathews, Newkirk, and Eichenberger], SILT [Davis and Clark], I [Johnson], and many more. The constraint solver is essentially the same in all these systems because it allows only Manhattan constraints and solves those in x independently from those in y, thereby reducing the problem to one dimension. Also, these systems always restrict their constraints to simple inequalities between only two component coordinates. Thus the constraints left by 3 or more and above by 5 can be expressed, but complex expressions such as right by the same distance as that from A to B cannot be handled.
With all of these restrictions, solution is simple: The constraints for a given axis are sorted by dependency, and values are substituted in order. If the constraints A left of B by 5 or more and B left of C by 6 are given, then C is the least constrained and the first to be given a value. Subsequent values are set to be as small as possible, so that, once a position is established for C, B will be to it's left by 6 and A will be to it's left by 11. It is possible to rewrite all constraints in terms of C (as EARL does) or simply to solve the system by working from C to B and then to A. When two constraints appear for the same variable, the larger value is used to keep all constraints valid. So, for example, if the additional constraint A left of C by 12 is given, then it will override the spacing of 11 from the other two constraints. Of course, constraints may conflict, which will cause unknown results. EARL can detect this situation because it rewrites the constraints before solving them, and then arrives at a nonsensical constraint of the form A left of A by X. Other systems will merely place objects incorrectly.
Although these constraints appear to be simple, they do form a powerful basis for complex operations. ALI, for example, has the primitive relationships inclusion, minimum size, separation, and attachment, which are all built on simpler inequalities [Lipton et al.]. It is also possible to use this kind of constraint system to compact a design to minimal design-rule spacing [Mathews, Newkirk, and Eichenberger; Hsueh and Pederson; Williams; Mosteller; Sastry and Klein]. All that is needed is to incorporate the design rules as implicit constraints between the edges of objects. Many of these systems also allow additional user constraints.
The preceding discussion presumes that constraints must be sequentially executed in order to be solved. Sequential execution techniques are called propagation. There are, however, a number of satisfaction techniques that work in parallel. The Juno system has a simple enough set of constraints that each one can be expressed algebraically and the entire collection can be placed into a system of simultaneous equations that is solved with Newton-Raphson iteration [Nelson].
More complex systems of constraints can be solved in parallel by using a method called relaxation. In this method, each constraint has an error function that indicates the degree to which the constraint is satisfied. Changes are made to every object in an attempt to achieve a minimum total constraint error. However, since it may not be possible to satisfy all constraints completely, the error functions may still be nonzero. Thus relaxation iterates between evaluating the error function and adjusting the constrained objects. Termination occurs when all error functions are zero or when the values cease to improve. As an example of this, the constraint system of Fig. 8.7 can be solved with the error and adjusting functions in Fig. 8.8. The very first graphical constraint system, Sketchpad, used relaxation to solve its constraints [Sutherland].
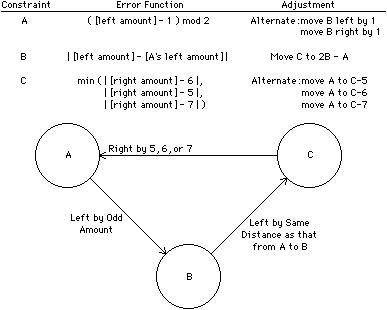 |
| FIGURE 8.8 Relaxation solves complex constraints. Solution steps: (1) Initialize: A-to-B = 1 [error = 0], B-to-C = 1 [error = 0], C-to-A = 2 [error = 3]. (2) Adjust constraint C: move A left by 3. Now: A-to-B = 4 [error = 1], B-to-C = 1 [error = 3], C-to-A = 5 [error = 0]. (3) Adjust constraints A and B: move B left by 1; move C right by 1. Now: A-to-B = 3 [error = 0], B-to-C = 3 [error = 0], C-to-A = 6 [error = 0]. |
The problem with relaxation is that it is slow. This is because of its iteration and the fact that every object in the system must be checked, regardless of whether it is affected by constraint change. The ThingLab system attempts to improve response time by dynamically compiling the constraints [Borning]. Nevertheless, relaxation and all other parallel constraint-satisfaction methods suffer from the need to examine every object. Propagation methods work more efficiently because they do not need to spread to every object if the nature of the constraint application is localized to a small area of the design. This is important in VLSI design systems, which often have very large collections of objects to be constrained.
| Previous | Table of Contents | Next | Static Free Software |